Die Trigonometrie der 10. Klassenstufe Mathematik beschäftigt sich mit den Beziehungen zwischen Winkeln und Seitenlängen im Dreieck. Eine besondere Rolle spielen dabei rechtwinklige Dreiecke. Schülerinnen und Schüler lernen in der 10. Klasse die Grundlagen der Trigonometrie und einige Anwendungsfälle kennen.
Ein rechtwinkliges Dreieck ist ein Dreieck, bei dem genau ein Winkel 90° beträgt. In rechtwinkligen Dreiecken gelten bestimmte Regeln.
Schüler kennen bereits den Satz des Pythagoras, welcher die Beziehungen der Seitenlängen in einem rechtwinkligen Dreieck beschreibt: a² + b² = c², wobei c die Länge der Hypotenuse des Dreiecks ist.
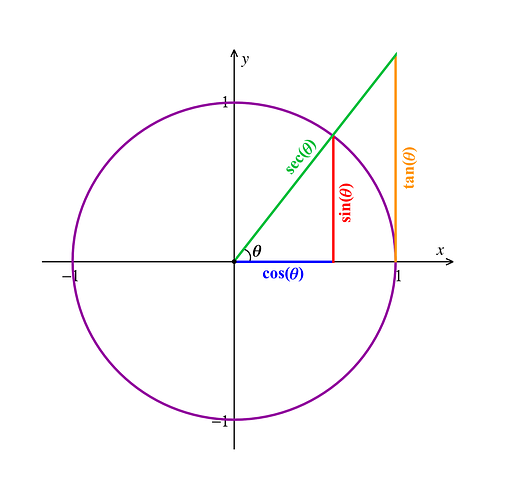
Nun lernen Schülerinnen und Schüler die Beziehungen der Winkel und Seitenlängen in einem rechtwinkligen Dreieck kennen. Dazu werden die grundlegenden trigonometrischen Funktionen eingeführt: Sinus (sin), Kosinus (cos) und Tagens (tan).
In rechtwinkligen Dreiecken gilt:
sin(α) = Gegenkathete/Hypotenuse
cos(α) = Ankathete/Hypotenuse
tan(α) = Gegenkathete/Ankathete
Durch Umformung und Gleichsetzung der obigen Gleichungen können jeweils fehlende Seitenlängen in rechtwinkligen Dreiecken berechnet werden, sofern ausreichend andere Werte zur Verfügung stehen.
Um hingegen die Winkel in rechtwinkligen Dreiecken zu berechnen, verwendet man die Umkehrfunktionen der trigonometrischen Funktionen: Arkussinus, Arkuskosinus und Arkustangens. Diese finden in Aufgabenstellungen anwendung, wenn Seitenlängen gegeben sind und Winkelgrößen berechnet werden sollen.
Winkel werden in der Trigonometrie sowohl in der Einheit Grad(°), als auch in der Einheit Bogenmaß angegeben und verwendet. Die Umrechnung erfolgt, indem man den Winkel in Grad mit dem Faktor (π / 180) multipliziert: Bogenmaß = Grad × (π / 180)
Zahlreiche praktische Anwendungsbeispiele der Trigonometrie finden sich beispielsweise in der Navigation zur Berechnung von Entfernungen in der Seefahrt oder in der Luftfahrt. In der Raumfahrt werden trigonometrische Berechnungen beispielweise zur Berechnung von Umlaufbahnen verwendet. Auch in der Architektur, in der Akustik, für die Berechnung in Computerspielen und in verschiedenen Disziplinen der Physik und Ingenieurswissenschaften sind trigonometrische Funktionen ein Alltagswerkzeug für verschiedene Berechnungen.